1. 베이즈 정리(Bayes’ theorem)란?
'베이브 정리'는 확률 이론에서 중요한 개념 중 하나이다. 이는 18세기에 프랑스의 수학자인 피에르-시몽 라플라스에 의해 개발되었다. 베이브 정리는 사건 A가 발생했을 때 사건 B가 발생할 조건부 확률을 계산하는 방법이다.
간단히 말해서, P(A|B)로 표시되는 사건 B가 발생했을 때 사건 A가 발생할 확률은 P(A)와 P(B|A)의 곱으로 계산된다. 여기서 P(A)는 사건 A가 발생할 사전 확률이며, P(B|A)는 사건 A가 발생했을 때 사건 B가 발생할 조건부 확률이다.
수학적으로는 다음과 같이 표현된다.

여기서 는 사건 A와 사건 B가 동시에 발생할 확률을 나타내며, 는 사건 B가 발생할 확률이다.
베이브 정리는 확률 이론과 통계 분야에서 다양한 응용을 가지고 있으며, 조건부 확률을 계산할 때 유용하게 사용된다.
2. 베이즈 정리 쉽게 이해하기
평소 호감이 있던 상대에게 초콜릿을 선물 받았다.
나에게 호감이 있어서 준 것일까? 아니면 예의상 준 것일까?
상대방이 나에게 호감이 있어서 초콜릿을 줬는지 베이즈 정리를 통해 계산해보자.
먼저 이유 불충분의 원리에 따라, 상대방이 나를 좋아할 확률을 50%, 좋아하지 않을 확률을 50%라고 가정해보자.
이유 불충분의 원리(Principle of Indifference)
무관심의 원칙이라고도 불리며, 다른 사건보다는 하나의 사건을 기대할 만한 어떤 이유가 없는 경우에는 가능한 모든 사건에도 동일한 확률을 할당해야 한다는 원칙이다.
상대방이 나를 좋아할 확률 50%에서 새로운 정보를 근거로 객관적인 확률로 업데이트 시켜보자.
한 설문조사를 통해 좋아하는 사람에게 초콜릿을 줄 확률이 40%라는 것을 알고 있다고 가정해보자.
그렇다면, 호감이 있지만 초콜릿을 주지 않을 확률은 자동으로 60%가 된다.
호감이 없는 사람에게도 30%가 예의상 초콜릿을 준다고 가정해보자.
여기서도, 호감이 없는 사람에게 초콜릿을 주지 않을 확률은 자동으로 70%가 된다.
첫 번째 정보
좋아하는 사람에게 초콜릿을 줄 확률(40%)
'좋아하는 사람에게'라는 조건이 있으므로, 이를 '조건부 확률'이라 부른다.
호감이 있지만 초콜릿을 주지 않을 확률(60%)
두 번째 정보
호감이 없는 사람에게 초콜릿을 줄 확률(30%)
마찬가지로, '호감이 없는 사람에게 '라는 조건이 있으므로, 이를 '조건부 확률'이라 부른다.
호감이 없는 사람에게 초콜릿을 주지 않을 확률(70%)
이해를 돕기 위해, 100명의 사람이 있다고 가정해보자.
이유 불충분의 원리에 따라 50명은 누군가의 호감을 얻고 있고, 50명은 인기가 없다.
호감을 얻고 있는 50명 중에서 40%인 20명은 초콜릿을 받을 것이다.
그렇지만, 누군가의 관심을 받고 있어도 50명의 60%인 30명은 초콜릿을 받지 못한다.
인기가 없는 50명 중 30%, 즉 15명은 예의상 초콜릿을 받고 헛된 희망을 품을 수도 있다.
반면, 나머지 70%인 35명은 초콜릿을 받지 못한다.
우리가 알고 싶은 것은 '초콜릿을 받았을 때, 초콜릿을 준 사람이 날 좋아할 확률'이다.
이것은 우리가 알고 있는 좋아하는 사람일때, 초콜릿을 줄 확률의 조건과 결과가 뒤바뀐 것이다.
초콜릿을 못 받은 상황은 우리의 관심사가 아니기 때문에 제거한다.

위에서 봤던 베이즈 정리 수식이다. 우리가 얻은 정보를 통해 계산해보자.
는 사건 A와 사건 B가 동시에 발생할 확률을 나타내며, 호감을 얻고있고, 초콜릿을 받은 사람이 해당된다.
는 사건 B가 발생할 확률이며, 초콜릿을 받은 사람이 해당된다.

'이유 불충분의 원리'에 따라 상대방이 나를 좋아할 확률 50%에서, 7% 상승한 57%로 업데이트되었다.
여기서, 아무런 정보 없이 50%라고 가정했던 값을 '사전 확률(Prior Probability)'이라 부른다.
새로운 정보를 근거로 업데이트 된 57%의 값을 '사후 확률(Posterior Probability)'이라 부른다.
사전 확률을 바탕으로 사후 확률을 얻는 것, 이것이 '베이즈 정리'이다.
베이즈 정리의 이러한 특징은 셜록 홈즈의 명대사로 표현할 수 있다.
불가능한 경우를 제외하고 남은 것은 아무리 이상하고 믿기지 않더라도 사실이기 마련이야.
3. 베이즈 정리를 그림으로 이해하기
베이즈 정리는 좀 더 쉽게 이해하는 것은 상황을 사각형으로 시각화하는 것이다.
이 사각형으로 복잡한 수식을 사용하지 않고, 베이즈 정리의 핵심을 이해할 수 있다.
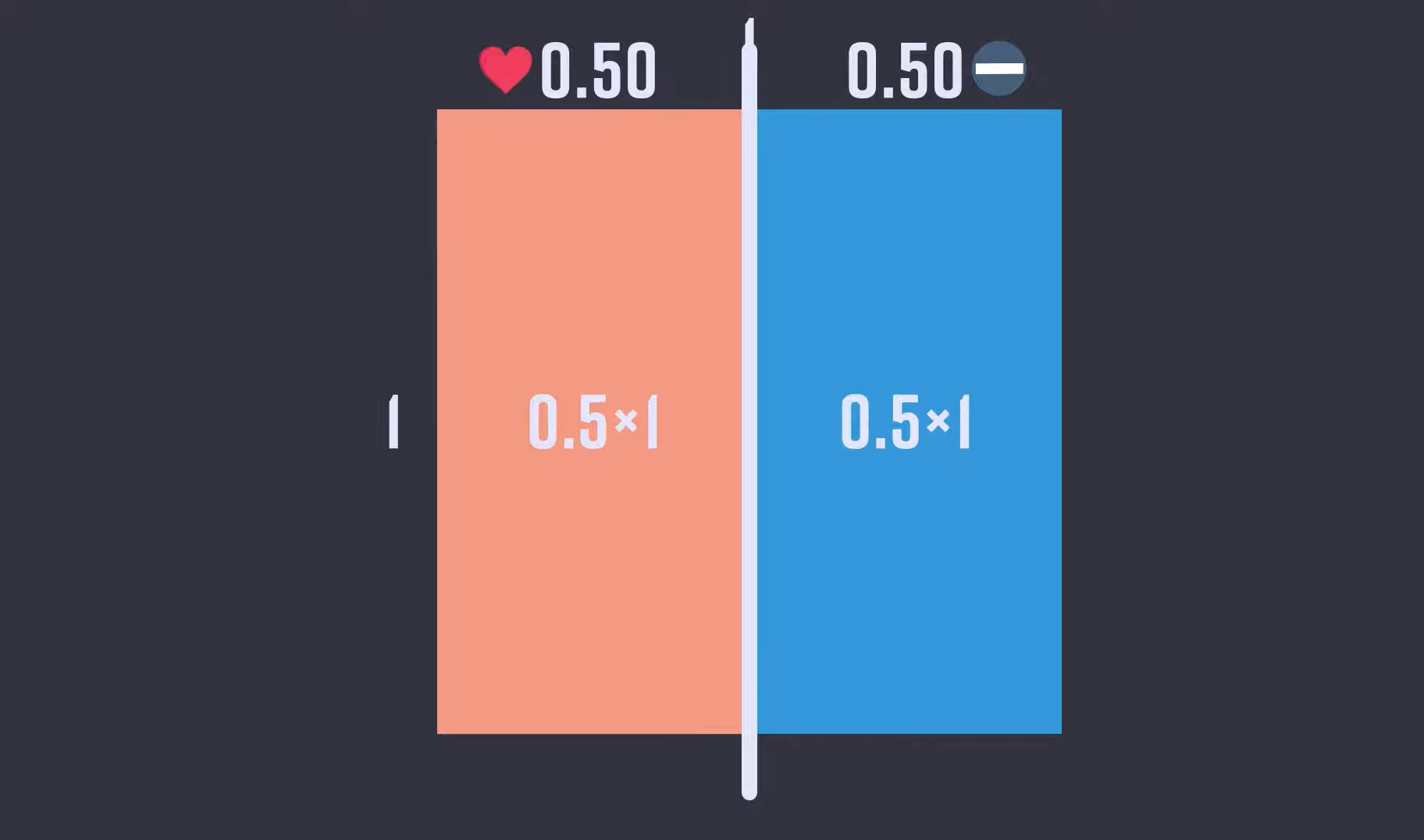
사각형의 가로와 세로를 각각 1이라고 가정한다.
넓이는 가로와 세로의 길이를 곱한 1이 된다. 즉, 사각형의 넓이 1은 전체 확률 100%를 의미한다.

'이유 불충분의 원리'를 통해 '사전 확률'을 설정한다.
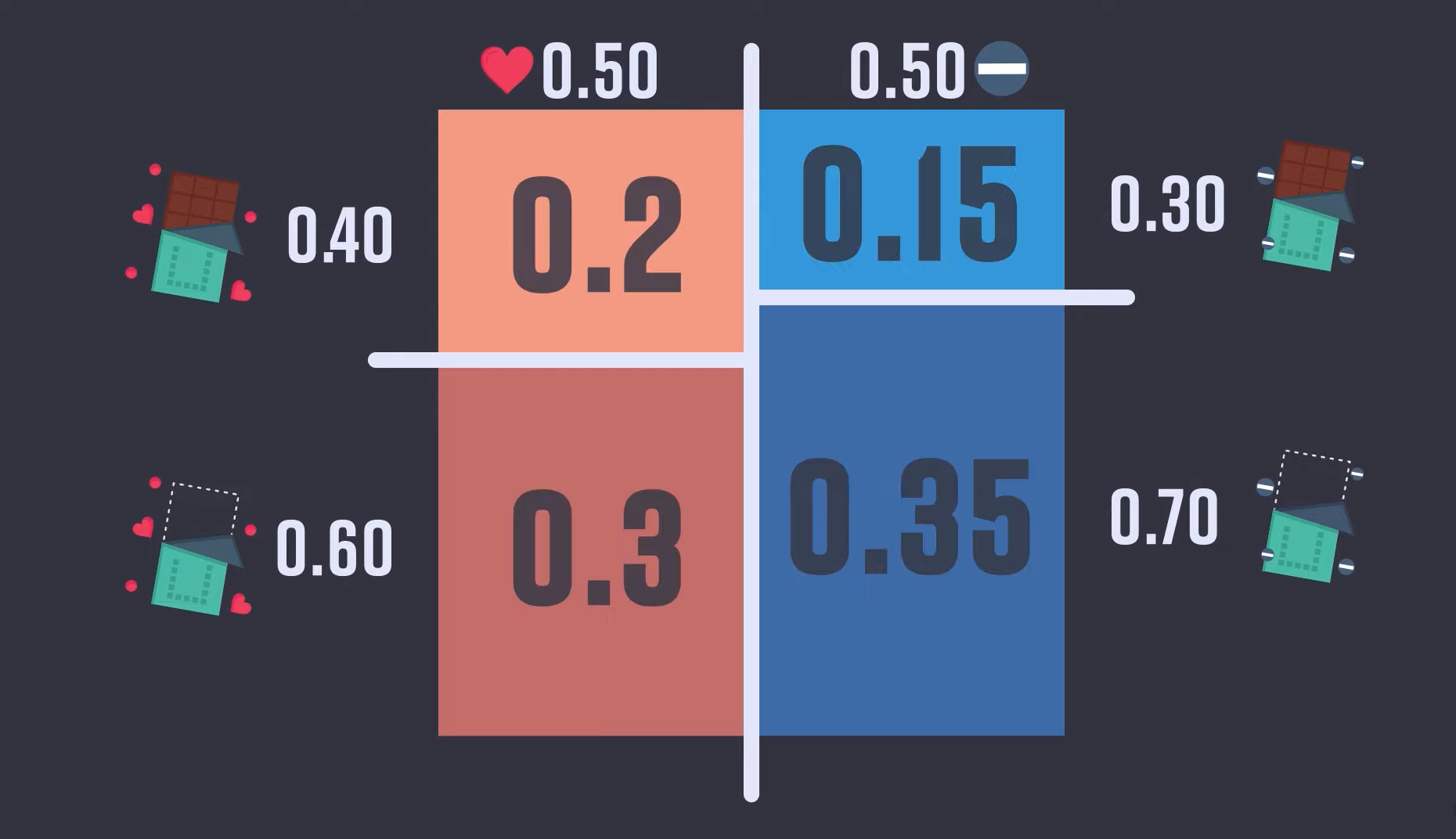
각각의 정사각형의 넓이를 계산하면 아래의 그림과 같다. 작은 사각형들의 넓이 자체가 확률이 된다.
초콜릿을 받은 상황만을 남겨보자.
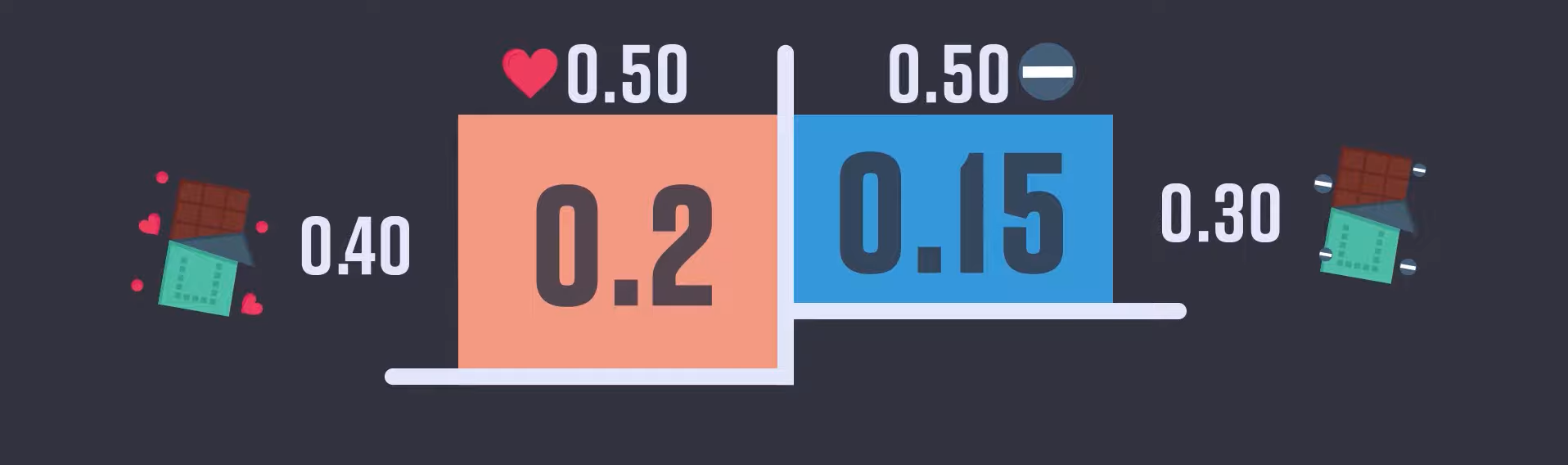
초콜릿을 받은 영역들의 확률을 계산해보면,
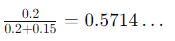
앞에서와 동일한 57%라는 '사후 확률(Posterior Probability)'을 구할 수 있다.
하지만이 계산 과정이 조금은 수상하게 느껴질 수도 있다. 바로 '사전 확률(Prior Probability)'이라는 초기의 믿음 때문이다.
이러한 주관적 요소로 인해 베이즈 이론은 수학자들로부터 비난을 받기도 했다. 그러나 우리는 새로운 정보와 관찰을 근거로 객관적인 확률로 업데이트 시켜 나간다. 베이즈 정리는 데이터가 많을 수록 올바른 의사결정을 내릴 확률이 높아진다. 초콜릿을 받을 사건뿐 아니라 단 둘이 식사를 한 사건, 밤늦게까지 통화를 한 사건 등을 바탕으로 사전 확률을 지속적으로 업데이트 하는 것이다. 이것이 베이즈 정리의 중요한 통찰이다.
이는 사람의 의사결정 과정이기도 하며, 경영학의 '린 방식'이라 불리는 접근과도 닮아있다.
현대에서 베이즈 정리는 인공지능의 의사결정에 매우 강력한 도구로 위력을 발휘하고 있다.
해당 포스팅은 아래의 출처를 바탕으로 정리했습니다.
https://www.youtube.com/watch?v=Y4ecU7NkiEI&list=PL7_MtvxhoNAwVx8Dm1MkSNaivIQcQFaqi&index=1
'통계 > 베이즈 정리' 카테고리의 다른 글
| 영화 추천 알고리즘, 나이브 베이즈 분류 (0) | 2024.03.14 |
|---|

댓글